|
|

|
|
MATH
Astronomers could not measure the distance to Venus and the Sun without using a geometric principle well-known to land surveyors:
Triangulation. Astronomers use a modified version of this principle. To find the distance to a planet or other astronomical object, instead
of measuring the base angles A and B which is what a surveyor would do, you measure the vertex angle, P. For the transit of Venus,
observers on the Earth at A and B will be separated by thousands of miles. Venus will appear at different places on the distant Sun. By
measuring the angle shift between the two spots on the Sun in degrees, you can determine the vertex angle, and from the baseline
distance A to B, determine the distance to Venus. 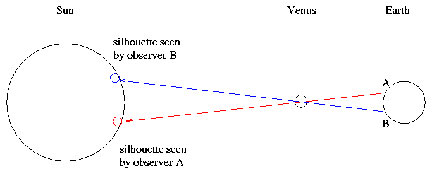
Suppose it was hard for you to measure the two base angles in the triangulation method. This could easily happen if the object were
so far away that your instrument could not accurately discern that these angles were different than 90 degrees. For example, if the
object is 10 miles away, and your baseline is only 5 feet long, the two base angles would have a measure of 89.9946 degrees. This angle
differs from 90 degrees by only 0.0044 degrees which equals 16 seconds of arc (there are 60 minutes or arc/degree x 60 seconds of
arc/minute of arc = 3600 seconds of arc per degree!) This would be a very difficult angle to measure even with very expensive modern
surveying equipment!
To solve this problem, astronomers don't bother measuring the base angles at all. Instead, they measure the vertex angle in the triangle.
It turns out that this angle is very easily measured using photographic techniques. The method is called trigonometric parallax or just
'parallax' for short. Here's how it works:
Extend your arm in front of you, hold your thumb up, and alternately open and close your eyes. You will see your thumb's position move
against the more distant background in front of you.
In 1663, Rev. James Gregory who was an astronomer and mathematician considered, suggested that a more accurate measurement of the
Earth-Sun distance could be made. He showed how this distance could be measured from observations of the transit of Venus made from
various widely separate geographical locations. A few years later, Sir Edmund Halley, made the same suggestion in 1677, and published
the details of this technique in 1716. Sir Edmund Halley described in detail how scientists from various nations could observe the upcoming
1761 and 1769 transits of Venus from many parts of the world. From the parallax shifts they would measure, they would be able to measure
this distance from the Earth to Venus and the sun with near-perfect accuracy.
The TRACE satellite orbits Earth and has its sensors trained on the surface of the Sun to search for solar flares. The changing perspective of
the location of Mercury in its orbit also leads to a parallax shift. Below is a close-up of the consecutive images of Mercury taken every 450
seconds as it traveled across the sun on May 7, 2003:

Notice that the track of mercury across the sun moves slightly up and down in a sinusoidal pattern. This is due to the changing location of the TRACE satellite as it orbits earth. If you want to analyze this image to determine the distance to the sun from earth, visit the activity "Calculating the Astronomical Unit during a Transit of Mercury using Satellite Data" (http://image.gsfc.nasa.gov/poetry/venus/TRACEmerc.html)
developed by Dr. Sten Odenwald (NASA/IMAGE) and Dr. Bart DePontieu (Lockheed Martin/TRACE)
After the transit of venus, look for the companion Venus parallax activity
(http://image.gsfc.nasa.gov/poetry/venus/TRACEvenus.html)
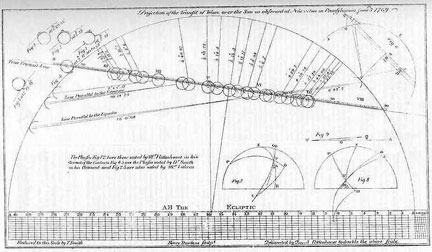
This drawing is from the June 3,1769
transit of Venus, and shows the details
of the path across the sun at that time.
No two observers at different latitudes
will see the path cross in exactly the
same places.
|
|



![]()